Manacher's Algorithm: Longest Palindromic Substring

Saturday, February 27, 2016

Overview

One of the most interesting algorithms is to find the longest palindromic substring in O(n) time. A palindrome is a string that is the same when reversed. For example, Dr. Awkward is a palindrome. If we remove non alphanumeric characters and make each character lower case, it becomes drawkward which is the same thing spelled backwards. For more information, you can look at Manacher’s Algorithm wiki page.

Content

Below is a video that explains the algorithm very well, but I made a quick summary for myself and for you guys.

Summary

Animated

The reason why the less efficient algorithm on the left runs in O(n^2) time is because we have to expand the palindrome from length = 0 for every single character in the string. That’s the only thing stopping us from reaching the algorithm on the right which runs in O(n).

The animation is made by Taro Kuriyama who makes amazing visualizations. Click the animation to go to his own blog post about palindromes.



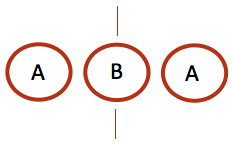
Odd Palindrome

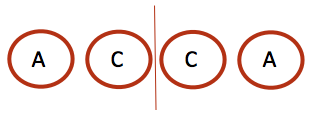
Even Palindrome

A palindrome’s center can either be at the position of a character (for palindromes of odd length) or between two characters (for palindromes of even length)

Symmetric Palindrome

To make the process of finding the palindrome easier without worrying about odd or even substrings, we place a # character between each letter. We also place two different symbols at the front and back of the array to make it easier to compute the sides.



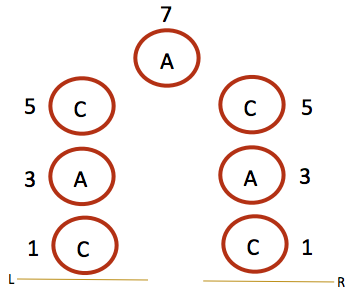
Symmetric Palindrome

A Palindrome’s sides are symetric while in its boundries, but not past its boundaries. When we count R - A's index, we also count the spaces in between the two letters as shown in the image below.

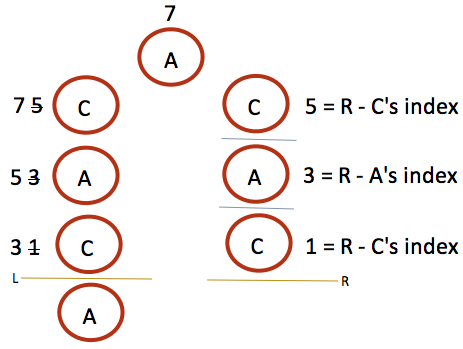
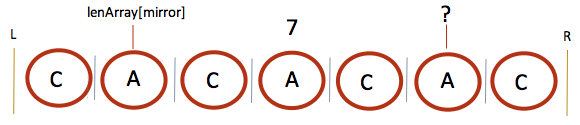
Symmetric Palindrome



Symmetric Palindrome

So we need two rules for finding ?.

  1. If lenArray[mirror] goes beyond the L boundary, ? = R - ?’s index. if (mirror - lenArray[mirror] < L) { ? = R - ?'s index }

  2. If lenArray[mirror] is within the L boundary, ? = lenArray[mirror]. if (mirror - lenArray[mirror] >= L) { ? = lenArray[mirror]}

Descriptive Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

public int manachers(String s) {
    // [$, #, a, #, b, #, a, #, @]
    char[] processed = processString(a);
    int[] palins = new int[processed.length];
    int c = 0; // center
    int r = 0; // right bound
    
    int biggest = 0;
    int biggestCenter = 0;
    
    for (int i = 1; i < processed.length - 1; ++i) {
        int mirror = getMirrorIndex(c, i);
        
        if (isIndexWithinRightBoundary(i, r)) {
            int distanceFromBoundary = r - i;
            int mirrorValue = palins[mirror];
            palins[i] = Math.min(distanceFromBoundary, mirrorValue);
        }
        
        while (canGrowPalindrome(processed, palins, i)) {
            expandPalindromeAtIndex(palins, i);
            if (palins[i] > biggest) {
                biggest = palins[i];
                biggestCenter = i;
            }
        }
        
        if (currentPalinPassedRightBoundary(i, palins, r)) {
            c = i;
            r = i + palins[i];
        }
    }
    // or return biggest to get the length of the longest palindrome
    return getPalindrome(biggest, biggestCenter, a);
}

public String getPalindrome(int len, int pos, String s) {
    pos = pos/2;
    pos -= len/2;
    pos -= (len % 2 == 1) ? 1 : 0;
    return s.substring(pos, pos + len);
}

/**
 *        l     c     r
 * [$, #, a, #, b, #, a, #, @]
 * [0, 0, 1, 0, 1, 0, 0, 0, 0]
 */
private boolean canGrowPalindrome(char[] arr, int[] palins, int center) {
    char left = arr[center + (1 + palins[center])];
    char right = arr[center - (1 + palins[center])];
    return left == right;
}


/**
 *     l <=     c     => r
 * [$, #, a, #, b, #, a, #, @]
 * [0, 0, 1, 0, 2, 0, 0, 0, 0]
 */
private void expandPalindromeAtIndex(int[] palins, int index) {
    ++palins[index];
}

private boolean currentPalinPassedRightBoundary(int index, int[] palins, int rightBoundary) {
    int newBoundary = index + palins[index];
    return newBoundary > rightBoundary;
}

private boolean isIndexWithinRightBoundary(int index, int rightBoundary) {
    return index < rightBoundary;
}

private int getMirrorIndex(int center, int index) {
    return 2*center - index;
}

private char[] processString(String s) {
    StringBuilder sb = new StringBuilder("$#");
    for (char c : s.toCharArray()) {
        sb.append(c);
        sb.append("#");
    }
    sb.append("@");
    return sb.toString().toCharArray();
}

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

public int manachers(String s) {
    char[] chars = process(s);
    int[] palins = new int[chars.length];

    int c = 0;
    int r = 0;
    int biggest = 0;

    for (int i=1; i < chars.length-1; ++i) {
        int mirror = 2*c - i;

        if (i < r) {
            palins[i] = Math.min(r-i, palins[mirror]);
        }

        while (chars[i + (1 + palins[i])] == chars[i - (1 + palins[i])]) {
            ++palins[i];
        }

        if (palins[i] > biggest) {
            biggest = palins[i];
        }

        if (i + palins[i] > r) {
            c = i;
            r = i + palins[i];
        }
    }
    return biggest;
}

Random Posts