Union Find

Overview

The Union-Find Disjoint Set data structure is very interesting. The UFDS is used to model several disjoint (not connected) sets and is in the domain of percolation theory. It allows you to find if an object is in the same set as another and which set an object should be or is in. This has some very cool and useful applications like Kruskal’s algorithm to find the minimum spanning tree of a graph. It can also be used social networks in the form of friend circles.

Content

We have a group of Disjoint Sets and we want to group them together. To do this, we need two operations: find and union.

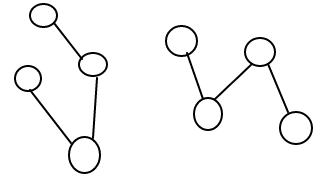
Disjoint Sets

Find will determine what set an element is in while union will create the union of two elements.

Internal Data Structure

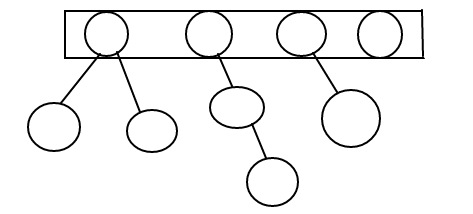
We’re going to create a forest.

Each set will be a tree and have a representative element (the root of the tree).

Sets

1
2
3
4
5
6
public class Node<T> {
    T value;
    String name;
    Node<T> parent;
    Node<T>[] children;
}

Find

The find operation on a node N will simply walk up the tree and find its root R. You can then compare other representative elements to R to determine which set N belongs to. This runs in O(log n) where n is the number of elements in the set and the tree is balanced.

1
2
3
4
5
6
public Node<T> find(Node<T> node) {
    while (node.getParent() != null) {
        node = node.getParent();
    }
    return node;
}

Union

For the union operation, we will find both the elements’ roots and put them together and return the resulting representative element. Which runs in O(log n) where n is the number of elements in the set and the tree is balanced.

1
2
3
4
5
6
7
public Node<T> union(Node<T> first, Node<T> second) {
    first = find(first);
    second = find(second);

    first.setParent(second);
    second.addChild(first);
}