Overview
You’re a doctor at a hospital’s ER and you have many patients to see. There are too many patients to see, so you decide to make a queue program. The patients put their name in the program and they get added to the end of the queue.
That works, but it’s not right. Not every patient should be treated the same. In the event that one patient has a stomach ache while another has a gunshot wound, this system would give them priority on a first come first serve basis.
We need a priority queue. The priority queue will place people inside the queue based on their priority. A patient with a gunshot wound has more priority than someone who has a stomach ache. How do we make a priority queue? It’s implemented as a heap data structure.
Content
What does a heap look like?
Structure
First, we have to know that a heap is a complete binary tree.
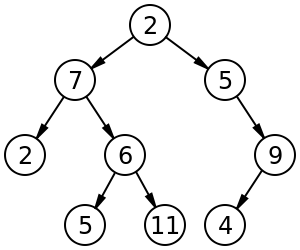
In a binary tree, a node has at most two child nodes.
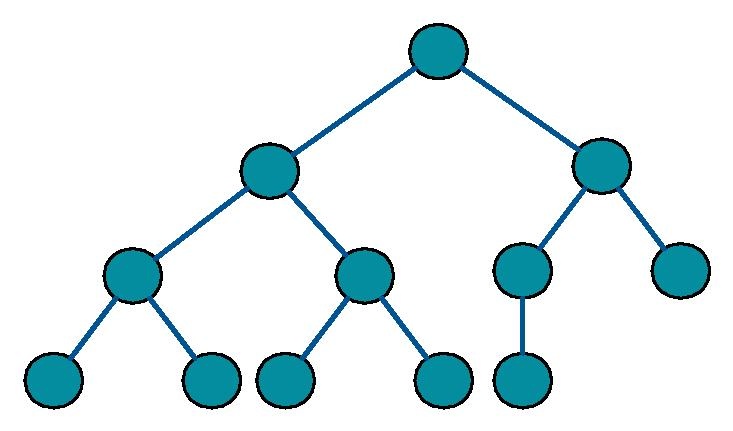
In a complete binary tree, every level except the last level must be filled (have two children).
There are two types of heaps: a min-heap and a max-heap.
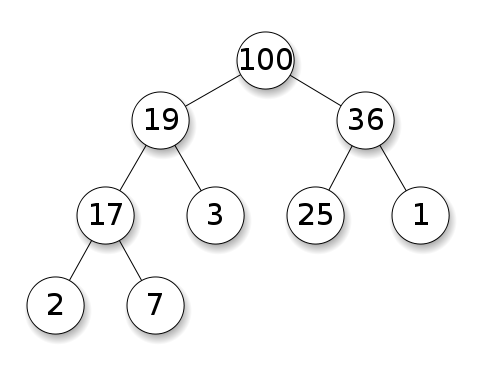
In a max-heap, the parent node must have a higher value than its two child nodes.
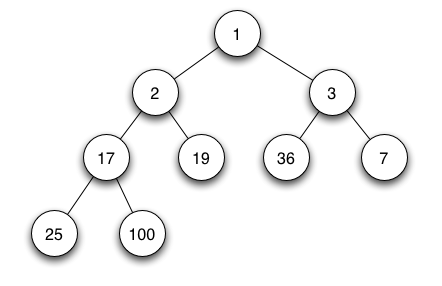
In a min-heap, the parent node must have a lower value than its two child nodes.
Insertion
When we add a new node, we add at the right most position on the lowest level.
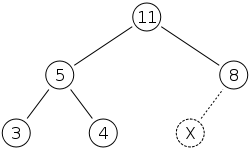
Let’s say we add a node X with value 15.
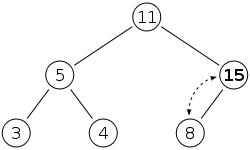
We violated the heap property (the value of the parent must be bigger than the values of its children). The parent with value 8 has a child with a value of 15. To maintain the heap property, we swap them or bubble up.
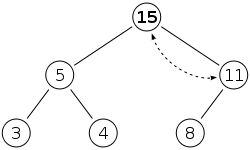
The property is still violated so we must swap or bubble up again. We’re done. We don’t need to look on the left side because that side was already correct.
Deletion
When we remove a node, we go through 3 steps.
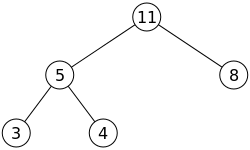
Remove root 11 and return it
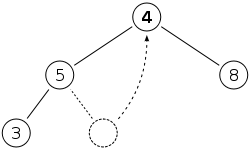
Take last node inserted (right most on the lowerst level) and put it as the root
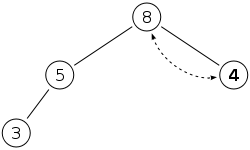
We bubble down
Conclusion
This is a basic overview of the heap datastructure. I will talk about the heap’s implementation and the heap sort in another post!