Longest Common Subsequence

Overview

The longest common subsequence is an old algorithm problems. You might ask yourself what applications it might have. Well 2 very important applications of the LCS are file comparison and molecular biology. Read on to find out how it works. You can also look at the wiki and the visualization tool to better understand.

Content

What is the longest common subsequence? Given 2 strings, the LCS finds the longest ordered sequence of characters that is common to both strings, appear in the same order but are not necessarily contiguous. Here’s an example.

sequence X: ABCDEFG sequence Y: BCDGK

The sequence B -> C -> D -> G is the longest common subsequence. Those characters appear in both strings in that order.

Solution

The longest common subsequence is a dynamic programming question. I will make another post about how to approach and solve dynamic programming questions in another post. The solution runs in O(n^2)

One of the ways to solve a dynamic programming question is by first building a table bottom up with the solutions to the subproblems and then building the solution from the table.

Building the table

Our table will have the following dimensions.

1
2
3
int rows = firstString.length() + 1;
int cols = secondString.length() + 1;
int[][] table = new int[rows][cols];

This is how we’re going to populate the table. Like all the other dynamic programming problems, we use the precomputed values to compute the next value.

1
2
3
4
5
6
7
8
9
for (int row=1; row < rows; ++row) {
    for (int col=1; col < cols; ++col) {
        int diagCell = table[row-1][col-1] + sameCharacters;
        int topCell = table[row-1][col];
        int leftCell = table[row][col-1];

        table[row][col] = Math.max(diagCell, Math.max(topCell, leftCell));
    }
}

This generates the following table.

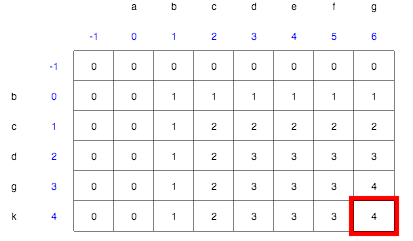
We know that the Longest Common Subsequence has a length of 4. The reason why a cell would increase in value is because there was a char in the first string that matched a char in the second string as defined by our variable ‘sameCharacters’;

int sameCharacters = (firstString.charAt(row-1) == secondString.charAt(col-1))? 1 : 0;

Generating the solution from the table

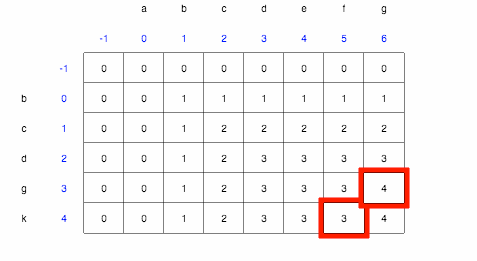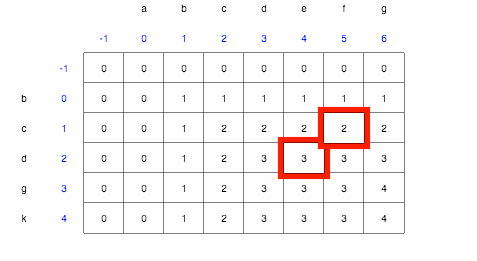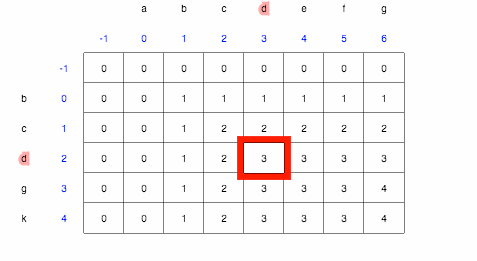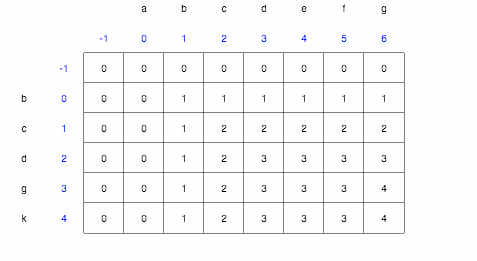
Given our table, we will use the following rules to generate the solution.

1. Start at the bottom right corner, the largest value.
2. If firstString.charAt(row) is the same as secondString.charAt(col), then we add the letter to the front of our solution, go to the top right corner cell
3. Otherwise, go to the cell that has the biggest value between the top cell and the left cell.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public static String lcs(String first, String second) {
    int rows = first.length() + 1;
    int cols = second.length() + 1;
    int[][] table = new int[rows][cols];
    
    for (int row=1; row < rows; ++row) {
        for (int col=1; col < cols; ++col) {
            int same = (first.charAt(row-1) == second.charAt(col-1))? 1 : 0;
            int diag = table[row-1][col-1] + same;
            int top = table[row-1][col];
            int left = table[row][col-1];
            table[row][col] = Math.max(diag, Math.max(top, left));
        }
    }
    return buildSolutionFromTable(table, first, second);
}

public static String buildSolutionFromTable(int[][] table, String first, String second) {
    int row = first.length();
    int col = second.length();
    StringBuilder result = new StringBuilder();
    
    while (row > 0 && col > 0) {
        char letter1 = first.charAt(row-1);
        char letter2 = second.charAt(col-1);
        
        if (letter1 == letter2) {
            result.insert(0, letter1);
            --row;
            --col;
        } else if (table[row-1][col] > table[row][col-1]) {
            --row;
        } else {
            --col;
        }
    }
    return result.toString();
}